Rule of 72: The Foundation of Doubling Calculations – Your Complete Guide to Smart Investment Planning

When I first started my investment journey, I was overwhelmed by complex calculations and financial formulas that seemed impossible to understand.

Then I discovered the Rule of 72, and everything changed. This simple yet powerful tool transformed how I look at my investments and helped me make better financial decisions without needing a calculator every time.

The Rule of 72 is a mental math shortcut that tells you how long it takes for your money to double at a given interest rate. You simply divide 72 by your annual return percentage. For example, if your investment earns 8% annually, it will double in approximately 9 years because 72 divided by 8 equals 9.

I use this calculation almost daily when evaluating investment opportunities, and it has saved me countless hours of complex calculations.

What makes this rule so valuable is its simplicity and accuracy. When I compare my Rule of 72 estimates with actual compound interest calculations, the results are remarkably close for interest rates between 6% and 10%.

This range covers most common investment scenarios, from mutual funds to fixed deposits, making it incredibly practical for everyday use.

Also Read: Best Investment Growth And Timeline Rules That You Should Know

Key Takeaways

• The Rule of 72 estimates doubling time by dividing 72 by the annual interest rate
• Works best for compound interest rates between 6% and 10% with high accuracy
• Applies to investments, inflation calculations, debt growth, and economic projections
• Formula is derived from natural logarithms but simplified for easy mental math
• Has minor limitations at extreme interest rates but remains practical for most scenarios
• Can be reversed to find required return rates for specific doubling timeframes

Who Invented Rule of 72 and Its Mathematical Foundation

I often get asked who invented the Rule of 72, and the answer is fascinating. While its exact origins remain somewhat mysterious, most financial historians credit Italian mathematician Luca Pacioli, who described it in his 1494 book Summa de Arithmetica. However, the concept likely existed in various forms even earlier among merchants and money lenders.

The beauty of this rule lies in its mathematical derivation. The actual formula for doubling time comes from the compound interest equation. When you solve for the time needed to double your money, you get a result involving natural logarithms where ln of 2 equals approximately 0.693. This means the precise doubling time is 69.3 divided by the interest rate.

However, 72 was chosen instead of 69.3 for a very practical reason. I appreciate this choice because 72 is easily divisible by many common numbers including 2, 3, 4, 6, 8, 9, and 12. This divisibility makes mental calculations much simpler when working with typical interest rates. The small sacrifice in precision is worth the gain in usability.

Benefits of Rule of 72 in Real World Applications

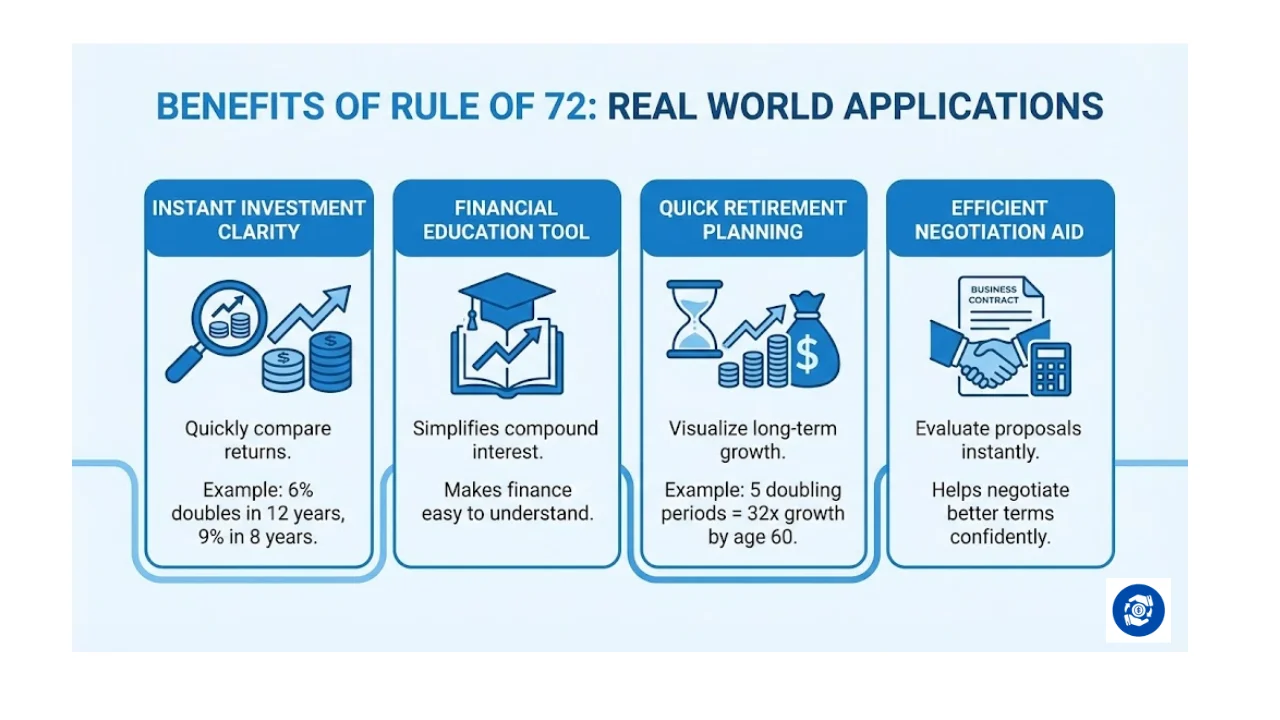
Through my years of working with personal finance, I have discovered numerous benefits of the Rule of 72 that make it indispensable.

First and foremost, it provides instant clarity when comparing investment options. When my bank offers me a 6% return and another institution offers 9%, I can immediately see that one doubles my money in 12 years while the other does it in 8 years.

The rule also serves as an excellent educational tool. I have taught this concept to countless people who previously found finance intimidating.

Once they understand that their money at 7% annual return doubles roughly every 10 years, the power of compound interest becomes tangible and real.

Another significant benefit I have experienced is using this rule for quick retirement planning. If you start investing at age 25 with a 10% average return, your money doubles around every 7 years. By age 60, that is five doubling periods, meaning your initial investment grows 32 times. This visualization helps me stay motivated during market downturns.

The Rule of 72 also excels in negotiation scenarios. When evaluating business loans or investment proposals, I can quickly calculate the long term impact without appearing to struggle with mathematics. This instant calculation ability has helped me make better decisions and occasionally negotiate better terms.

Where to Use Rule of 72 for Maximum Impact

I apply the Rule of 72 across multiple financial scenarios almost daily. In investment planning, it helps me set realistic expectations. When someone claims they can consistently deliver 20% returns, I know that would double money every 3.6 years, which is extraordinarily rare and potentially suspicious.

For retirement accounts like provident funds and pension plans, I use this rule to project future values. If my retirement fund earns 8% annually, I can quickly estimate how my current balance will grow over the next 20 or 30 years by counting the number of doublings. This helps me determine whether I am on track for my retirement goals.

Credit card debt is another critical area where I use this rule. With interest rates around 18% on many cards, unpaid balances double approximately every 4 years. This calculation has helped me counsel many people about the urgency of paying off high interest debt before focusing on lower return investments.

I also apply this rule when analyzing business growth rates. If a company is growing revenue at 15% annually, that revenue doubles roughly every 4.8 years. This helps me evaluate whether growth stocks are reasonably priced based on their expansion trajectory.

Rule of 72 Inflation and Purchasing Power Protection

Understanding Rule of 72 inflation applications has been crucial for my long term financial planning. Inflation works in reverse compared to investments, it halves your purchasing power instead of doubling your money. At a 3% inflation rate, your money loses half its value in approximately 24 years.

I remember when inflation in some periods reached 6% annually. Using the Rule of 72, I calculated that prices would double every 12 years, meaning a product costing 100 rupees would cost 200 rupees in just over a decade. This realization pushed me to seek investments that beat inflation by a comfortable margin.

The inflation application becomes even more critical when planning for major expenses decades away. If you are saving for your child’s education 18 years from now, and education inflation runs at 8%, costs will roughly double twice during that period. What costs 10 lakh rupees today will cost around 40 lakh rupees then.

I use this calculation to stress test my financial plans. If my investments grow at 10% but inflation runs at 6%, my real return is only 4%, meaning my purchasing power doubles every 18 years rather than every 7 years. This perspective prevents me from becoming overly optimistic about nominal returns.

Rule of 72 Formula Variations and Accuracy

The standard Rule of 72 formula is simple. Years to double equals 72 divided by annual interest rate percentage.

However, I have learned that slight variations exist for different scenarios. The Rule of 69.3 provides more mathematical accuracy since ln of 2 is 0.693, but I rarely use it because the extra precision does not justify the more difficult mental math.

For continuous compounding situations, the Rule of 69 works slightly better. I encountered this when analyzing certain bonds and derivative products that use continuous compounding. However, for most retail investors, the difference between rules of 69, 69.3, and 72 is negligible.

When interest rates fall below 5% or rise above 15%, I notice the Rule of 72 becomes less accurate. At 2% interest, the rule suggests 36 years to double, but the actual time is closer to 35 years. At 20% interest, it suggests 3.6 years, but reality is closer to 3.8 years. Despite these minor variations, I still find it useful for quick estimates.

I have also discovered you can reverse the formula to find required returns. If you want to double your money in 10 years, you need approximately 7.2% annual returns because 72 divided by 10 equals 7.2. This reverse application helps me set realistic investment targets.

Limitations of Rule of 72 and When to Use Alternatives

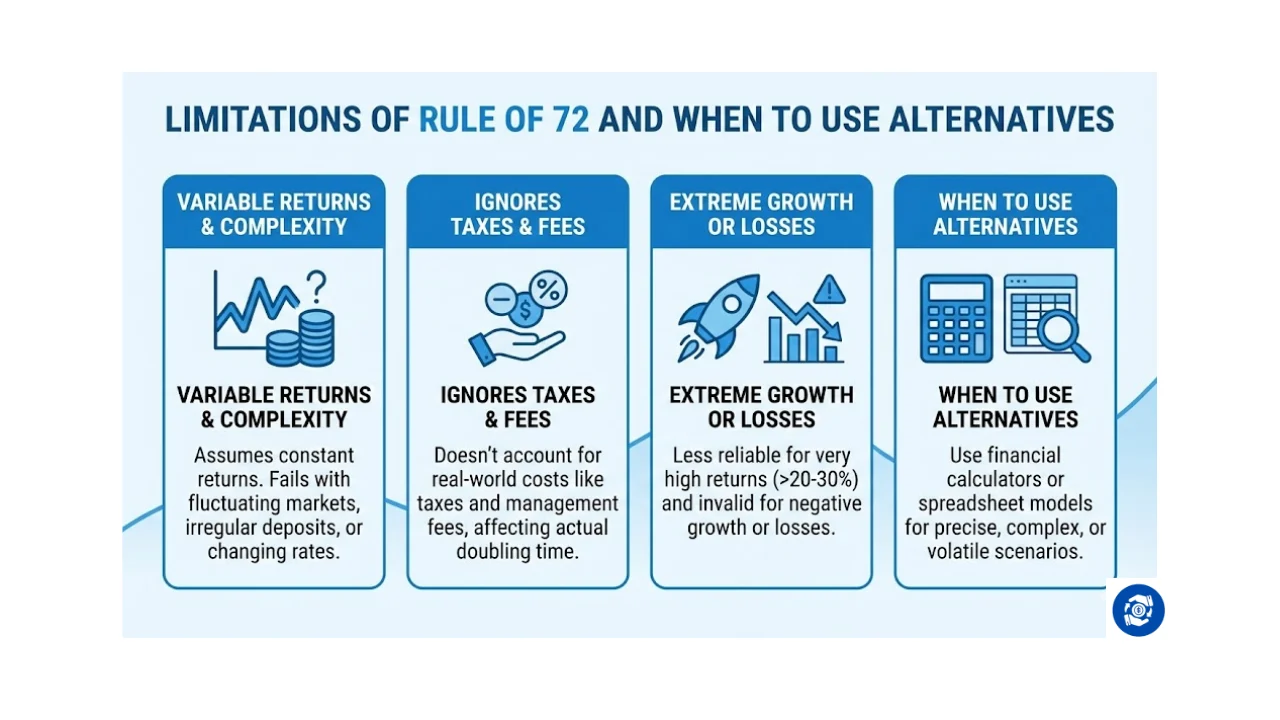
Despite my enthusiasm for this tool, I acknowledge the limitations of Rule of 72 that every investor should understand.

The primary limitation is its assumption of constant returns. In reality, investment returns fluctuate year to year. My stock portfolio might return 15% one year and lose 5% the next, making the actual doubling time different from the Rule of 72 prediction.

The rule also ignores taxes and fees. When I calculate that my 8% return doubles money in 9 years, I am not accounting for capital gains tax, transaction fees, or fund management charges.

After taxes and fees, my effective return might be only 6%, changing the doubling time to 12 years instead.

Another limitation I have encountered is with very high growth investments. When evaluating startup equity or cryptocurrency, returns can be extremely volatile and potentially much higher than 20-30%. At these extreme rates, the Rule of 72 becomes less reliable, and I switch to more precise compound interest calculations.

The rule does not work for negative growth or losses. If your investment loses 10% annually, you cannot simply divide 72 by negative 10. Instead, I use different formulas to calculate how long until the investment halves in value, which requires understanding exponential decay rather than growth.

For complex scenarios involving variable contributions, irregular deposits, or changing interest rates, I recognize that the Rule of 72 falls short. In these cases, I turn to financial calculators or spreadsheet models that can handle multiple variables and provide more accurate projections for sophisticated planning needs.

Tags: rule of 72, investment doubling time, compound interest calculation, financial planning tools, wealth building strategy, inflation impact calculator, retirement planning formula

About Author